Predicting Play Type on Third Down

Summary

For our assignment, we are interested in trying to predict the type of play that will be called on third down in a given NFL game. Third down conversions are one of the key metrics that can measure a team’s success and win probability.

Report can be found here, slides here and relevant code can be found in this GitHub repo.

Data and Methods

We used a dataset from Kaggle containing every event (play or otherwise) for every NFL game between the years 2009 and 2017. The dataset contains a total of 102 features, ranging from date and score to touchdown probability and win probability. After performing feature selection, we implemented different models and found that a Random Forest model captures the nuances in the data the best.

The five models studied were:

• Decision Trees
• Random Forest
• Logistic Regression
• K-Nearest Neighbors
• Gaussian Naive Bayes

All models were set to the default scikit-learn parameters, except for Logistic Regression which we passed with L1 and L2 regularization. To evaluate the models we utilized the Area Under the ROC (AUC) curve metric and after establishing which model performed best, we dove deeper into the model’s hyperparameters to maximize the AUC.

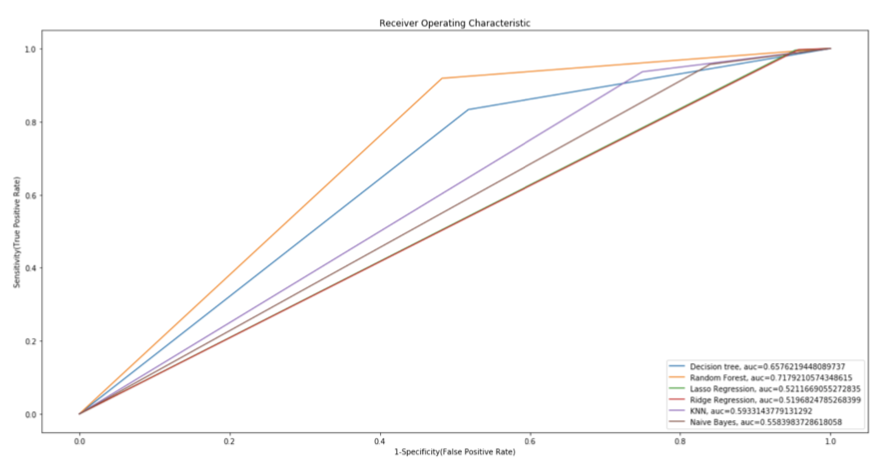
The Random Forest model captures the nuances in the data the best. Random Forests can handle all sorts of data without the need to scale or change their types and they are especially good when trying to learn a specific data set. They have high variance, as they are very sensitive to sampling error, but come with low bias, as they can learn the given data as you let the forest grow. NFL decision making is nuanced and scenario dependent: teams who are leading tend to run late in games, teams losing tend to pass more, teams close to their own goal line run to minimize the risk of a safety, etc. This means multiple decision trees working as an ensemble are a good prediction candidate.

Random Forests are as close as it comes to a “free lunch” in Data Science: they decrease the variance of individual trees, without increasing bias, by using bootstrap aggregation. This selects multiple random samples with replacement from the training set, fits a tree to each one and predicts on the unseen examples by a majority vote classification.

Another big advantage of Random Forests is that they naturally allow us to rank feature importance by computing out-of-sample error before and after permuting a feature.

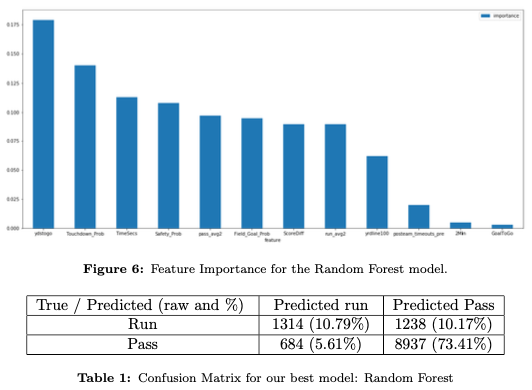
While the ‘Two Minute Warning’ binary variable does not make a big difference, both running and passing moving averages, add information to the model.

The confusion matrix is concentrated mostly along the diagonal, as the model has a 84.21% accuracy, a 87.83% precision and a 92.21% recall. By further exploring the available features, it is possible the model could be improved. However, the fact that we are achieving these metrics on an unbalanced class after reducing the features by 90%, speaks to the power of using Random Forests for this particular problem.